NPB 163/PSC 128
Simulating differential equations
Discrete-time systems
- In most real physical systems, such as neurons, time is
continuous. Thus, we use mathematical constructs such as
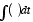 and
and 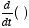 to represent summation and differences over continuous time, which is infinitely
divisible.
to represent summation and differences over continuous time, which is infinitely
divisible.
- If we wish to simulate such systems on a digital computer,
then we have no choice but to discretize time. Note however that this is
not true of all computation in general. Analog computers, which
pre-dated the digital computers we have today, serve as very useful simulation
tools for studying complex dynamical systems using op-amps and capacitors
without the need to discretize time.
- In the digital computer, we represent the continuous-time
signal
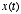 by sampling at discrete points in time:
by sampling at discrete points in time:
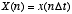
where 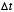 is the sampling interval and n is the sample number (an integer).
Thus,
is the sampling interval and n is the sample number (an integer).
Thus, 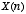 represents a sample of
represents a sample of 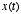 at time
at time 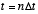 . Note that the sampling interval
. Note that the sampling interval 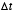 must be picked sufficiently small so as to capture the significant time-varying
structure in
must be picked sufficiently small so as to capture the significant time-varying
structure in 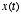 , otherwise aliasing will result (this is what makes wagon wheels
and propellers look like they’re sometimes moving backwards in movies).
, otherwise aliasing will result (this is what makes wagon wheels
and propellers look like they’re sometimes moving backwards in movies).
Difference equations
- A discrete-time approximation to the derivative is computed
by taking the difference between adjacent samples divided by the sampling
interval:
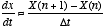
In the limit as 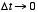 , this relationship becomes an equality (by definition).
, this relationship becomes an equality (by definition).
- Now lets say we wish to simulate the differential equation
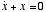 . Re-expressing this as a discrete-time difference equation, we have
. Re-expressing this as a discrete-time difference equation, we have
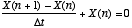 .
.
With a little algebraic manipulation of terms, we obtain
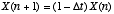
Thus, to simulate this system on a computer, we simply run a loop for 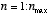 and set X to a fraction
and set X to a fraction 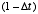 of its previous value at each iteration. Note however that if we pick
of its previous value at each iteration. Note however that if we pick 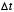 too large, then the system will not decay to zero but rather explode to
too large, then the system will not decay to zero but rather explode to
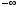 . In this case, we must have
. In this case, we must have 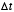 <1 since
<1 since 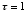 .
.
- In a similar fashion, we can simulate the leaky-integrator
with time-constant

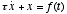
via the difference equation
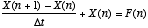
which results in the discete-time equation
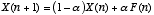
where 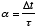 and
and 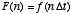 . Note again though that in order for this simulation to work we must have
. Note again though that in order for this simulation to work we must have
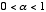 , and so
, and so 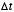 must be picked to be small relative to
must be picked to be small relative to  .
.
- The discete-time version of the leaky integrator gives
us another perspective on what it is computing. Here we see that at each
time step, the next value of X is a weighted sum of the current value
of X and the current value of the input F. The weights that
are used to combine X and F add to one. Thus, if
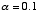 then the next value of X is 90% of its current value plus 10% of
the current value of F. It is easy to show that this recursive computation
is equivalent to taking an expontentially decaying weighted sum of the present
and past values of F.
then the next value of X is 90% of its current value plus 10% of
the current value of F. It is easy to show that this recursive computation
is equivalent to taking an expontentially decaying weighted sum of the present
and past values of F.
- This method of simulating a differential equation is known
as Euler’s method. It is by far the simplest method of simulating
a differential equation. Its disadvantage though is that it only crudely
approximates the derivative, and so
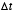 must be picked very small to obtain accurate simulations. A small
must be picked very small to obtain accurate simulations. A small 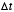 means that many iterations are required, which demands more time. More
efficient methods for simulating differential equations, such as the Runge-Kutta
method, achieve the same degree of accuracy with larger time steps and
hence fewer iterations.
means that many iterations are required, which demands more time. More
efficient methods for simulating differential equations, such as the Runge-Kutta
method, achieve the same degree of accuracy with larger time steps and
hence fewer iterations.
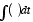 and
and 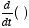 to represent summation and differences over continuous time, which is infinitely
divisible.
to represent summation and differences over continuous time, which is infinitely
divisible.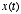 by sampling at discrete points in time:
by sampling at discrete points in time: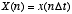
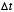 is the sampling interval and n is the sample number (an integer).
Thus,
is the sampling interval and n is the sample number (an integer).
Thus, 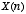 represents a sample of
represents a sample of 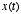 at time
at time 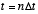 . Note that the sampling interval
. Note that the sampling interval 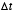 must be picked sufficiently small so as to capture the significant time-varying
structure in
must be picked sufficiently small so as to capture the significant time-varying
structure in 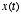 , otherwise aliasing will result (this is what makes wagon wheels
and propellers look like they’re sometimes moving backwards in movies).
, otherwise aliasing will result (this is what makes wagon wheels
and propellers look like they’re sometimes moving backwards in movies).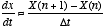
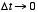 , this relationship becomes an equality (by definition).
, this relationship becomes an equality (by definition).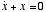 . Re-expressing this as a discrete-time difference equation, we have
. Re-expressing this as a discrete-time difference equation, we have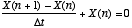 .
.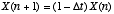
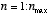 and set X to a fraction
and set X to a fraction 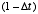 of its previous value at each iteration. Note however that if we pick
of its previous value at each iteration. Note however that if we pick 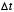 too large, then the system will not decay to zero but rather explode to
too large, then the system will not decay to zero but rather explode to
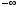 . In this case, we must have
. In this case, we must have 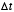 <1 since
<1 since 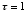 .
.
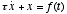
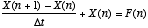
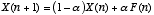
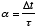 and
and 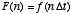 . Note again though that in order for this simulation to work we must have
. Note again though that in order for this simulation to work we must have
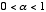 , and so
, and so 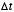 must be picked to be small relative to
must be picked to be small relative to  .
. 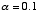 then the next value of X is 90% of its current value plus 10% of
the current value of F. It is easy to show that this recursive computation
is equivalent to taking an expontentially decaying weighted sum of the present
and past values of F.
then the next value of X is 90% of its current value plus 10% of
the current value of F. It is easy to show that this recursive computation
is equivalent to taking an expontentially decaying weighted sum of the present
and past values of F.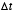 must be picked very small to obtain accurate simulations. A small
must be picked very small to obtain accurate simulations. A small 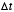 means that many iterations are required, which demands more time. More
efficient methods for simulating differential equations, such as the Runge-Kutta
method, achieve the same degree of accuracy with larger time steps and
hence fewer iterations.
means that many iterations are required, which demands more time. More
efficient methods for simulating differential equations, such as the Runge-Kutta
method, achieve the same degree of accuracy with larger time steps and
hence fewer iterations.