NPB 163/PSC 128
Dynamics
Differential equations
- Dynamics is essentially the study of how things change
over time. This is important for understanding the brain, because we are
constantly being inundated with time-varying signals. How neurons respond
to these signals over time is the essence of what neural coding is all about.
- Differential equations simply provide a mathematical
description for how things change over time. The central element of a differential
equation is the time-derivative of a variable,
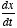 . This essentially tells us the rate of change of the variable x,
where x(t) may be voltage, position of a particle, etc.
. This essentially tells us the rate of change of the variable x,
where x(t) may be voltage, position of a particle, etc.
- The derivative can have different orders:
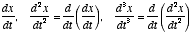 , etc. For example, if x is position, then
, etc. For example, if x is position, then 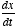 will be its velocity and
will be its velocity and 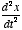 its acceleration.
its acceleration.
- A first-order differential equation would have terms
of the form x and
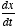 . A second-order differential equation would have terms of the form
x,
. A second-order differential equation would have terms of the form
x, 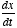 , and
, and 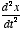 . Or in general, an
. Or in general, an 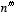 -order differential equation would have terms of the form x,
-order differential equation would have terms of the form x, 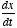 ,...
,... 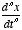 .
.
- The simplest kind of differential equation is a linear
differential equation, which simply contains derivatives of different
orders, each multiplied by a constant:
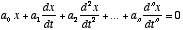
- Oftentimes, we denote a time-derivative using the “dot”
notation
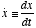 . Thus, in this notation, a second-order linear differential equation would
have the form
. Thus, in this notation, a second-order linear differential equation would
have the form
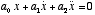
Exponential decay
- The very simplest differential equation would be a first-order,
linear differential equation:
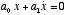
- When
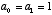 , then we have the simple relation
, then we have the simple relation 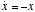 . What this tells us is that the rate of change of x depends on the
value of x. If x is currently a large positive value, then
x will decrease quickly. If x is currently a negative
value, then x will increase, etc. Is there a mathematical equation
that will tell us explicitly how x changes as a function of time?
. What this tells us is that the rate of change of x depends on the
value of x. If x is currently a large positive value, then
x will decrease quickly. If x is currently a negative
value, then x will increase, etc. Is there a mathematical equation
that will tell us explicitly how x changes as a function of time?
- It turns out that the general solution to the above equation
is of the form
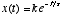
where the constant k is determined by the initial condition, or the
initial state of x at t=0, and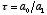 . For example, if x(0)=1 and
. For example, if x(0)=1 and 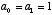 , then we have
, then we have 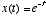 . Thus, a first-order linear differential equation describes the process
of exponential decay.
. Thus, a first-order linear differential equation describes the process
of exponential decay.
- The rate of decay is determined by the “time constant,”
 . If
. If  is large, then this means that x decays slowly. If
is large, then this means that x decays slowly. If  is very small, then x decays quickly. Basically, the way to think
of it is that when an amount of time
is very small, then x decays quickly. Basically, the way to think
of it is that when an amount of time  has gone by, the value of x will have been reduced by a factor of
1/e (the number e is about 2.7).
has gone by, the value of x will have been reduced by a factor of
1/e (the number e is about 2.7).
Leaky integrator
- So far, we have examined the case where the right-hand side
of the differential equation is zero. What if there is a time-varying function
on the right hand side? i.e.,
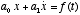
How does 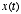 vary as a function of
vary as a function of 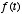 ?
?
- It turns out that the solution for
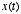 is now
is now
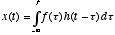
where the function 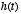 is the solution obtained when the right-hand side is zero. Thus, this equation
tells us that
is the solution obtained when the right-hand side is zero. Thus, this equation
tells us that 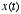 is simply a linearly weighted sum of the present and past values of
is simply a linearly weighted sum of the present and past values of 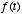 . The weights are given by the function
. The weights are given by the function 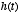 , which as we have seen above is an exponentially decaying function. So
the more recent values of
, which as we have seen above is an exponentially decaying function. So
the more recent values of 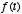 will be weighted more heavily than the present values, and values far in
the past will be entirely forgotten.
will be weighted more heavily than the present values, and values far in
the past will be entirely forgotten.
- Such a system is called a leaky integrator, because
the past leaks away from the summation of present and past values of
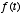 . We can think of
. We can think of 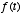 as the input to the system and
as the input to the system and 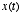 as the output of the system
as the output of the system
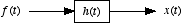
where 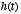 characterizes, via its time-constant, how far in the past that values of
characterizes, via its time-constant, how far in the past that values of
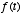 will affect the current value of
will affect the current value of 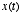 . Thus,
. Thus, 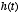 acts as a filter on the function
acts as a filter on the function 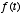 , smoothing over its details. If
, smoothing over its details. If  is large, then smoothing will be severe. If
is large, then smoothing will be severe. If  is small, little smoothing will occur.
is small, little smoothing will occur.
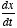 . This essentially tells us the rate of change of the variable x,
where x(t) may be voltage, position of a particle, etc.
. This essentially tells us the rate of change of the variable x,
where x(t) may be voltage, position of a particle, etc.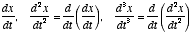 , etc. For example, if x is position, then
, etc. For example, if x is position, then 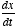 will be its velocity and
will be its velocity and 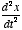 its acceleration.
its acceleration. 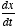 . A second-order differential equation would have terms of the form
x,
. A second-order differential equation would have terms of the form
x, 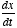 , and
, and 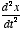 . Or in general, an
. Or in general, an 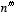 -order differential equation would have terms of the form x,
-order differential equation would have terms of the form x, 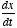 ,...
,... 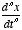 .
.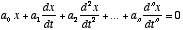
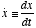 . Thus, in this notation, a second-order linear differential equation would
have the form
. Thus, in this notation, a second-order linear differential equation would
have the form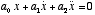
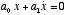
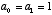 , then we have the simple relation
, then we have the simple relation 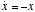 . What this tells us is that the rate of change of x depends on the
value of x. If x is currently a large positive value, then
x will decrease quickly. If x is currently a negative
value, then x will increase, etc. Is there a mathematical equation
that will tell us explicitly how x changes as a function of time?
. What this tells us is that the rate of change of x depends on the
value of x. If x is currently a large positive value, then
x will decrease quickly. If x is currently a negative
value, then x will increase, etc. Is there a mathematical equation
that will tell us explicitly how x changes as a function of time?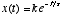
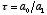 . For example, if x(0)=1 and
. For example, if x(0)=1 and 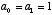 , then we have
, then we have 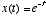 . Thus, a first-order linear differential equation describes the process
of exponential decay.
. Thus, a first-order linear differential equation describes the process
of exponential decay. . If
. If  is large, then this means that x decays slowly. If
is large, then this means that x decays slowly. If  is very small, then x decays quickly. Basically, the way to think
of it is that when an amount of time
is very small, then x decays quickly. Basically, the way to think
of it is that when an amount of time  has gone by, the value of x will have been reduced by a factor of
1/e (the number e is about 2.7).
has gone by, the value of x will have been reduced by a factor of
1/e (the number e is about 2.7).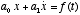
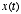 vary as a function of
vary as a function of 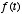 ?
? 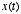 is now
is now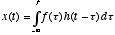
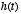 is the solution obtained when the right-hand side is zero. Thus, this equation
tells us that
is the solution obtained when the right-hand side is zero. Thus, this equation
tells us that 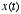 is simply a linearly weighted sum of the present and past values of
is simply a linearly weighted sum of the present and past values of 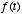 . The weights are given by the function
. The weights are given by the function 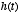 , which as we have seen above is an exponentially decaying function. So
the more recent values of
, which as we have seen above is an exponentially decaying function. So
the more recent values of 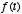 will be weighted more heavily than the present values, and values far in
the past will be entirely forgotten.
will be weighted more heavily than the present values, and values far in
the past will be entirely forgotten.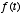 . We can think of
. We can think of 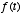 as the input to the system and
as the input to the system and 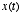 as the output of the system
as the output of the system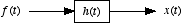
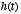 characterizes, via its time-constant, how far in the past that values of
characterizes, via its time-constant, how far in the past that values of
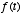 will affect the current value of
will affect the current value of 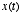 . Thus,
. Thus, 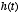 acts as a filter on the function
acts as a filter on the function 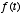 , smoothing over its details. If
, smoothing over its details. If  is large, then smoothing will be severe. If
is large, then smoothing will be severe. If  is small, little smoothing will occur.
is small, little smoothing will occur.