Psych/NPB 163
Fourier Analysis
Why frequency analysis?
- Many signals in the natural environment are conveniently described in terms of a superposition of wobbly functions (e.g., many sounds are produced by vibrating membranes).
- Sines and cosines are eigenfunctions of linear, time-invariant systems. Thus, they can be used to conveniently characterize the response of a linear system. Also, convolution, which is a complicated signal transformation in the time or space domain, is performed by simple multiplication in the frequency domain.
The Fourier series
- Joseph Fourier’s theorem, in its most general form, states that any function may be described in terms of a superposition of odd and even functions. Specifically, Fourier proposed that a signal may be decomposed into a summation of sinewaves of different frequencies, amplitudes and phases:
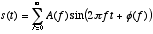 .
.
- What is remarkable about this is that
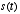 can be anything- the waveform produced by a bird chirping, the sound of your dishwasher, electromagnetic waves, etc.
can be anything- the waveform produced by a bird chirping, the sound of your dishwasher, electromagnetic waves, etc.
- The amplitudes
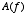 tell you how much of each frequency is present in the signal. For example, a pure tone (e.g., the waveform emitted by a tuning fork) would have
tell you how much of each frequency is present in the signal. For example, a pure tone (e.g., the waveform emitted by a tuning fork) would have 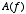 equal to zero for all frequencies except for one. The sound produced when you say “shhh” would have amplitudes distributed across many frequencies.
equal to zero for all frequencies except for one. The sound produced when you say “shhh” would have amplitudes distributed across many frequencies.
- The Fourier series tells us that a sound may be decomposed in terms of sinewaves, but it doesn’t tell us how to do it - i.e., it doesn’t tell us what amplitudes A to assign to each f. For this we need the Fourier transform.
The Fourier transform
- The Fourier transform basically provides a way of representing a signal in a different space - i.e., in the frequency domain. You put into the Fourier transform a function of time or space,
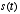 , and you get out a function of frequency,
, and you get out a function of frequency, 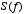 . The Fourier transform is formally defined as follows:
. The Fourier transform is formally defined as follows:
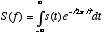 .
.
- Thus, the Fourier transform is essentially the inner-product of the signal
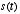 with the complex exponential
with the complex exponential 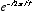 , evaluated at different values of f.
, evaluated at different values of f.
- The complex exponential is just a real cosine-wave and an imaginary sine-wave:
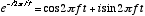 .
.
Thus, the Fourier integral may be written alternatively as
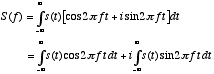
- Here we can see that
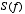 is a complex number. The real part tells us the result of multiplying our signal together with a cosine-wave, the imaginary part tells us the result of multiplying the signal together with a sine-wave.
is a complex number. The real part tells us the result of multiplying our signal together with a cosine-wave, the imaginary part tells us the result of multiplying the signal together with a sine-wave.
- The amplitude A of each frequency component contained in
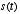 is given by the modulus of S, which is defined as
is given by the modulus of S, which is defined as
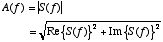
- The phase
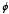 can be extracted from the ratio of the real an imaginary components of
can be extracted from the ratio of the real an imaginary components of 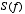 as follows:
as follows:
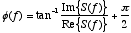
Convolution theorem
- The convolution of two functions,
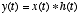
may be performed in the frequency domain via multiplication:
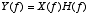 .
.
where 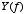 ,
, 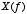 , and
, and 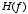 are Fourier transforms of
are Fourier transforms of 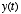 ,
, 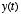 , and
, and 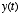 respectively.
respectively.
- That this is so is due to the fact that 1) sines and cosines are eigenfunctions of linear time-invariant systems, and 2) any function may be represented as a sum of sines and cosines.
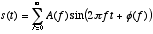 .
.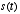 can be anything- the waveform produced by a bird chirping, the sound of your dishwasher, electromagnetic waves, etc.
can be anything- the waveform produced by a bird chirping, the sound of your dishwasher, electromagnetic waves, etc. 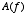 tell you how much of each frequency is present in the signal. For example, a pure tone (e.g., the waveform emitted by a tuning fork) would have
tell you how much of each frequency is present in the signal. For example, a pure tone (e.g., the waveform emitted by a tuning fork) would have 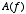 equal to zero for all frequencies except for one. The sound produced when you say “shhh” would have amplitudes distributed across many frequencies.
equal to zero for all frequencies except for one. The sound produced when you say “shhh” would have amplitudes distributed across many frequencies.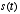 , and you get out a function of frequency,
, and you get out a function of frequency, 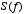 . The Fourier transform is formally defined as follows:
. The Fourier transform is formally defined as follows: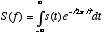 .
.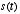 with the complex exponential
with the complex exponential 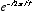 , evaluated at different values of f.
, evaluated at different values of f.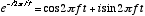 .
.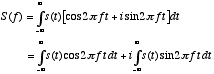
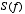 is a complex number. The real part tells us the result of multiplying our signal together with a cosine-wave, the imaginary part tells us the result of multiplying the signal together with a sine-wave.
is a complex number. The real part tells us the result of multiplying our signal together with a cosine-wave, the imaginary part tells us the result of multiplying the signal together with a sine-wave.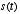 is given by the modulus of S, which is defined as
is given by the modulus of S, which is defined as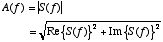
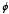 can be extracted from the ratio of the real an imaginary components of
can be extracted from the ratio of the real an imaginary components of 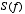 as follows:
as follows: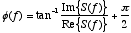
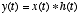
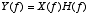 .
.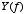 ,
, 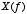 , and
, and 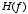 are Fourier transforms of
are Fourier transforms of 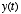 ,
, 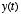 , and
, and 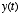 respectively.
respectively.