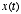 and output
and output 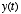 :
:
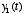 in response
to an input signal
in response
to an input signal 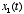 , and you later
observe an output
, and you later
observe an output 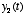 in response to
input
in response to
input 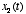 , then the response to the
combination
, then the response to the
combination 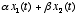 is just
is just 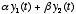 .
.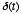 ,
where
,
where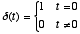
Let's call the output signal we measure in response to such an input 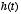 .
.
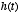 ,
we can compute the output
,
we can compute the output 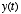 in response
to any complex input
in response
to any complex input 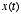 . The first
step is to consider the signal
. The first
step is to consider the signal 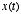 to be composed of a superposition of unit impulses of different amplitudes:
to be composed of a superposition of unit impulses of different amplitudes: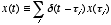
Now since the system is also time-invariant (i.e., it does not
change its behavior over time), then we know that the response to a shifted
impulse 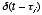 is just
is just 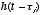 .
And so the response to a weighted sum of such shifted impulses is just
a weighted sum of the resulting shifted impulse response functions. Or
in the language of mathematics:
.
And so the response to a weighted sum of such shifted impulses is just
a weighted sum of the resulting shifted impulse response functions. Or
in the language of mathematics:
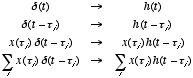
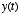 in response to
the input signal
in response to
the input signal 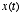 may be written
as
may be written
as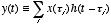 (1)
(1)
And in the limit that the spacing between time samples becomes infinitesimally small, this relation becomes exact and the sum turns into an integral:
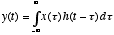 (2)
(2)
 symbol as follows:
symbol as follows: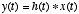
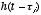 each of which is multiplied by
each of which is multiplied by 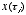 .
.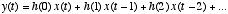
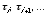 are spaced by one unit of time. Note also that we do not sum over values
of
are spaced by one unit of time. Note also that we do not sum over values
of 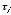 for which
for which 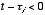 .
The reason is that for any physical system,
.
The reason is that for any physical system, 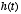 is defined only for
is defined only for 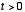 . This indeed
makes sense, because otherwise we would need to know future values of the
input in order to compute the present output.
. This indeed
makes sense, because otherwise we would need to know future values of the
input in order to compute the present output.
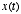 , where
the impulse response function
, where
the impulse response function 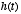 is
acting as the filter. The shape of
is
acting as the filter. The shape of 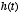 determines which properties of the original signal
determines which properties of the original signal 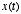 are "filtered out." The design of filters is usually best thought of in
the frequency domain, which we turn to next....
are "filtered out." The design of filters is usually best thought of in
the frequency domain, which we turn to next....