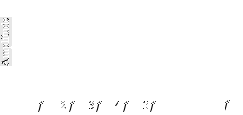1. One of the major cues that humans use to localize sound in azimuth is the interaural time difference (ITD) between left and right ears. However, for a pure tone, this cue is useful only for low frequencies. This is because at high frequencies, there is no longer a unique correspondence between the waveforms arriving at the left and right ear. Here, you will show why this is so.
a) First, figure out what would be the maximum time delay between left and right ears. For this, you will need the speed of sound in air and the distance between the two ears.
b) Now, plot the waveforms arriving at the left and right ear for a 500 Hz pure tone, assuming the sound is coming directly from the left (90 deg. from straight ahead).
c) Assuming that neurons spike only on the rising phase of each cycle of the waveform, plot the spike trains as they would appear on auditory nerve fibers tuned to 500 Hz.
d) If you were a neuron comparing these two spike trains, with no other knowledge about the environment (including the time of onset of the tone), how would you know which ear is closest to the sound source? And based on the time delay, where in space would you infer the sound to be?
e) Now repeat (b) and (c) for a 2000 Hz pure tone (and auditory nerve fibers tuned to 2000 Hz). Why is the direction of the sound source no longer unambiguous? What are the two alternative explanations for the observed shift in spike trains, and what (approximately) would be the corresponding directions in space for the sound source?
f) How might the neural circuits computing ITD overcome such ambiguity when using complex tones as stimuli?
2. Shown below is the spectrum of a complex tone with fundamental frequency
 .
.