Logs and music
Bruno A. Olshausen
Psych 129 - Sensory processes
Logarithmic scales provide a useful way to describe many types of natural phenomena. In the study of audition, logarithmic scales are used to describe sound intensity and frequency. This handout describes what a logrithm is, and why it appears so often in the study of audition.
The exponential function
To understand logarithms, you first need to understand exponential relationships. An integer exponent specifies how many times to multiply a number by itself. For example, 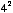 means
means 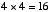 , and
, and 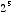 means
means 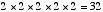 . If the exponent is negative, then this means the number is inverted and then multiplied by itself. For example,
. If the exponent is negative, then this means the number is inverted and then multiplied by itself. For example, 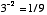 . Exponents can also be non-integer numbers. Here, the relationship is somewhat less intuitive--e.g.,
. Exponents can also be non-integer numbers. Here, the relationship is somewhat less intuitive--e.g., 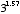 means “multiply 3 by itself 1.57 times,” so you get a number somewhere between 3 and 9 (more precisely, 5.6115). If the exponent is one divided by some integer n, then this means to take the n-th root of the number. For example,
means “multiply 3 by itself 1.57 times,” so you get a number somewhere between 3 and 9 (more precisely, 5.6115). If the exponent is one divided by some integer n, then this means to take the n-th root of the number. For example, 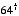 literally means “multiply 64 by itself 1/3 times,” or stated another way, “what number can you multiply by itself 3 times to get 64?” The answer in this case is 4.
literally means “multiply 64 by itself 1/3 times,” or stated another way, “what number can you multiply by itself 3 times to get 64?” The answer in this case is 4.
An exponential function is of the form 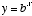 . This is plotted in figure 1 when b is 10. As you can see, y rises very rapidly for positive values of x, and decays slowly for negative values of x. You should reconcile this plot with the more intuitive relationships discussed in the paragraph above. Many things in nature exhibit either exponential growth or decay, so one often describes their dynamics with an exponential relationship such as
. This is plotted in figure 1 when b is 10. As you can see, y rises very rapidly for positive values of x, and decays slowly for negative values of x. You should reconcile this plot with the more intuitive relationships discussed in the paragraph above. Many things in nature exhibit either exponential growth or decay, so one often describes their dynamics with an exponential relationship such as 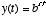 , where the value of c determines how fast things grow or decay depending on whether c is positive or negative, respectively.
, where the value of c determines how fast things grow or decay depending on whether c is positive or negative, respectively.
Figure 1: the exponential function
Logarithms
Now we are in a situation to understand what a logarithm is. A logarithm is basically the inverse of the exponential function. Thus, 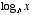 means, “the exponent to which you should raise b in order to obtain the number x.” In other words, we are asking
means, “the exponent to which you should raise b in order to obtain the number x.” In other words, we are asking 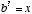 . The number b is known as the base of the logarithm. For example
. The number b is known as the base of the logarithm. For example 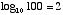 and
and 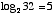 . The natural logarithm, often denoted ln, uses the number
. The natural logarithm, often denoted ln, uses the number 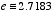 as its base. The function
as its base. The function 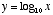 is plotted in figure 2. You should confirm by comparison with figure 1 that it is just the inverse of the exponential function--i.e., it’s the same function, just flipped on its side.
is plotted in figure 2. You should confirm by comparison with figure 1 that it is just the inverse of the exponential function--i.e., it’s the same function, just flipped on its side.
Figure 2: the logarithm function
One of the nice properties of the log function is that multiplication turns into addition, and division turns into subtraction. That is, if 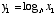 and
and 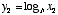 , then
, then
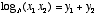
and
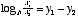
You should be able to prove these relationships for yourself given the relationship between the log and exponential functions. In the days before calculators, slide rules made mutiplication and division easy by using a logarithmic scale to represent numbers, and then sliding one scale against the other to add or subtract the logarithms, thus mutiplying or dividing, respectively, the numbers. It turns out that this property of the logarithm is also what makes it useful in describing sound intensity and frequency.
Sound intensity - the decibel scale
Alexander Graham Bell, the inventor of the telephone, observed that the difference in sound intensity that was needed to produce a perceptible change in the loudness of two tones increases proportional to the absolute intensity of the reference tone. That is, if you are comparing two very soft tones, then only a small change in intensity is need to perceive a difference. But if you are comparing two loud tones, then a larger change in intensity is needed to perceive the difference. Importantly, he found that the ratio of the intensities of the two tones needed to produce a perceptible difference was more or less constant, irrespective of the absolute intensity level one is at. Thus, a logarithmic scale provides a natural, intuitive way to describe sound intensity, because equal ratios, or equally discriminable sound levels, are converted to equal differences or intervals on the log-scale.
The ‘bel’ scale was named in Bell’s honor. It is just the base 10 logarithm of the ratio of intensity (power) of two sounds:
difference in bels = 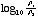
where 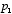 is the intensity of one sound and
is the intensity of one sound and 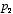 is the intensity of the other. Thus, a difference of 5 bels means that the ratio of sound intensities is 100,000. A ‘decibel’ is simply
is the intensity of the other. Thus, a difference of 5 bels means that the ratio of sound intensities is 100,000. A ‘decibel’ is simply 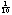 of a bel, and is denoted dB. Thus, a difference of 5 bels is the same as a difference of 50 decibels. Oftentimes the quantity one measures in an experiment is amplitude (for example, the amplitude of air pressure variations), and since power (what we have been loosely calling intensity) is proportional to the square of the amplitude, we have
of a bel, and is denoted dB. Thus, a difference of 5 bels is the same as a difference of 50 decibels. Oftentimes the quantity one measures in an experiment is amplitude (for example, the amplitude of air pressure variations), and since power (what we have been loosely calling intensity) is proportional to the square of the amplitude, we have
difference in decibels 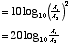
where 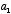 is the amplitude of one sound and
is the amplitude of one sound and 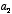 is the amplitude of the other.
is the amplitude of the other.
Frequency
As we learned in class, the basilar membrane has been constructed such that it resonates to different frequencies in different places. The representation of frequency along the basilar membrane is tonotopic, meaning that neighboring locations resonate to similar frequencies. Importantly, the representation is also approximately logarithmic, meaning that locations along the membrane separated by an equal amount of space have about the same ratio of their resonant frequencies. Assuming then that the 50,000 auditory nerve fibers innervate the basilar membrane in a roughly uniform manner along its length, the brain will receive a logarithmic representation of frequency as its input. The consequence, as it has been borne out in psychophysical experiments, is that humans rate the difference between tones according to the ratio of their frequencies. Tones that have similar frequency ratios tend to produce a similar percept of interval, irrespective of the absolute frequencies of the two tones being compared.
Frequency intervals are typically measured in terms of octaves. An octave is just a doubling in frequency. Thus, two tones separated by a factor of four in frequency would have a difference of two octaves. More formally, the relation is
difference in octaves = 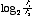 .
.
Thus, we can see that octaves are to frequency what decibels are to intensity. Equal frequency ratios translate into equal differences in terms of octaves.
Music
When you pluck a string, it vibrates at a certain frequency according to its length and tension, and these vibrations are sensed by the ear and relayed to the brain. If you pluck a bunch of strings together, it can either sound nice or downright awful, depending upon the frequency relationships among the strings. The modern piano has been designed to have an equally-tempered scale, meaning that the ratio between the frequencies of any two adjacent notes--for example, C to C#--is (approximately) the same no matter where you go on the keyboard. Thus, musical instruments have been designed around the logarithmic representation of frequency in the nervous system.
Two adjacent notes are referred to as a half-step, or semitone, and 12 half-steps make up an octave, or a doubling in frequency. (On the keyboard, an octave is when you go from one note to another that looks just like it above or below--see figure 3). Since the ratio between the frequencies of all half-steps are the same, then each adjacent pair will be separated by 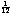 -octave, so the ratio between frequencies for each semitone is
-octave, so the ratio between frequencies for each semitone is 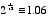 , or a 6% increase. Each time you raise a half-step, you multiply the frequency by about 1.06 to get the next note, and after you have done this 12 times you have multiplied by a factor of two. A full piano keyboard has 88 keys, and thus 7
, or a 6% increase. Each time you raise a half-step, you multiply the frequency by about 1.06 to get the next note, and after you have done this 12 times you have multiplied by a factor of two. A full piano keyboard has 88 keys, and thus 7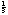 octaves, ranging from 27.5 Hz at the lowest A to 4186 Hz at the highest C.
octaves, ranging from 27.5 Hz at the lowest A to 4186 Hz at the highest C.
Figure 3: the piano keyboard
Perhaps one of the most interesting questions about music perception is why some intervals sound pleasing (consonant) and others sound harsh or difficult to bear (dissonant). A table of consonant intervals is shown below:
Interestingly, the consonant intervals all have integer-fraction frequency ratios. The consequence of this is that their harmonics will tend to either align or else produce other consonant frequency ratios. For example, the second harmonic of G will be 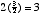 times the fundamental of C; thus, the second harmonic of G exactly aligns with the third harmonic of C. But this still doesn’t answer all of our questions. What if we were to just play two pure tones that don’t have any harmonics. We still get dissonance when they are next to each other in frequency. Why? The answer seems to be that it has something to do with critical bandwidth--i.e, the region over which frequencies significantly interact within a nerve fiber, which is about
times the fundamental of C; thus, the second harmonic of G exactly aligns with the third harmonic of C. But this still doesn’t answer all of our questions. What if we were to just play two pure tones that don’t have any harmonics. We still get dissonance when they are next to each other in frequency. Why? The answer seems to be that it has something to do with critical bandwidth--i.e, the region over which frequencies significantly interact within a nerve fiber, which is about 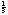 -octave. As shown in figure 4, the degree of perceived consonance between two tones depends on their relation to the critical bandwidth. If they are further apart than the critical bandwidth, then they are perceived to be consonant, but if within the critical bandwidth they are perceived dissonant. Of course as the two tones become even closer to one another they again become consonant. Thus, there seems to be a relation between dissonance and the bandwidth of frequency-tuned mechanisms in the cochlea and auditory nerve, but what interactions occur exactly that give rise to the percept of dissonance, and how this is processed and represented by the nervous system, is currently unknown.
-octave. As shown in figure 4, the degree of perceived consonance between two tones depends on their relation to the critical bandwidth. If they are further apart than the critical bandwidth, then they are perceived to be consonant, but if within the critical bandwidth they are perceived dissonant. Of course as the two tones become even closer to one another they again become consonant. Thus, there seems to be a relation between dissonance and the bandwidth of frequency-tuned mechanisms in the cochlea and auditory nerve, but what interactions occur exactly that give rise to the percept of dissonance, and how this is processed and represented by the nervous system, is currently unknown.
Figure 4: relation between consonance, dissonance and critical bandwidth
If you are interested further in this topic, I recommend reading “The Science of Musical Sound,” by John R. Pierce (W.H. Freeman & Co.).
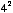 means
means 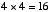 , and
, and 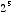 means
means 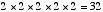 . If the exponent is negative, then this means the number is inverted and then multiplied by itself. For example,
. If the exponent is negative, then this means the number is inverted and then multiplied by itself. For example, 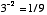 . Exponents can also be non-integer numbers. Here, the relationship is somewhat less intuitive--e.g.,
. Exponents can also be non-integer numbers. Here, the relationship is somewhat less intuitive--e.g., 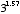 means “multiply 3 by itself 1.57 times,” so you get a number somewhere between 3 and 9 (more precisely, 5.6115). If the exponent is one divided by some integer n, then this means to take the n-th root of the number. For example,
means “multiply 3 by itself 1.57 times,” so you get a number somewhere between 3 and 9 (more precisely, 5.6115). If the exponent is one divided by some integer n, then this means to take the n-th root of the number. For example, 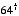 literally means “multiply 64 by itself 1/3 times,” or stated another way, “what number can you multiply by itself 3 times to get 64?” The answer in this case is 4.
literally means “multiply 64 by itself 1/3 times,” or stated another way, “what number can you multiply by itself 3 times to get 64?” The answer in this case is 4.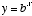 . This is plotted in figure 1 when b is 10. As you can see, y rises very rapidly for positive values of x, and decays slowly for negative values of x. You should reconcile this plot with the more intuitive relationships discussed in the paragraph above. Many things in nature exhibit either exponential growth or decay, so one often describes their dynamics with an exponential relationship such as
. This is plotted in figure 1 when b is 10. As you can see, y rises very rapidly for positive values of x, and decays slowly for negative values of x. You should reconcile this plot with the more intuitive relationships discussed in the paragraph above. Many things in nature exhibit either exponential growth or decay, so one often describes their dynamics with an exponential relationship such as 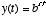 , where the value of c determines how fast things grow or decay depending on whether c is positive or negative, respectively.
, where the value of c determines how fast things grow or decay depending on whether c is positive or negative, respectively. 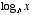 means, “the exponent to which you should raise b in order to obtain the number x.” In other words, we are asking
means, “the exponent to which you should raise b in order to obtain the number x.” In other words, we are asking 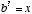 . The number b is known as the base of the logarithm. For example
. The number b is known as the base of the logarithm. For example 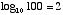 and
and 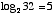 . The natural logarithm, often denoted ln, uses the number
. The natural logarithm, often denoted ln, uses the number 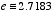 as its base. The function
as its base. The function 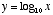 is plotted in figure 2. You should confirm by comparison with figure 1 that it is just the inverse of the exponential function--i.e., it’s the same function, just flipped on its side.
is plotted in figure 2. You should confirm by comparison with figure 1 that it is just the inverse of the exponential function--i.e., it’s the same function, just flipped on its side.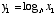 and
and 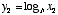 , then
, then 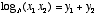
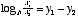
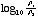
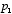 is the intensity of one sound and
is the intensity of one sound and 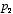 is the intensity of the other. Thus, a difference of 5 bels means that the ratio of sound intensities is 100,000. A ‘decibel’ is simply
is the intensity of the other. Thus, a difference of 5 bels means that the ratio of sound intensities is 100,000. A ‘decibel’ is simply 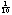 of a bel, and is denoted dB. Thus, a difference of 5 bels is the same as a difference of 50 decibels. Oftentimes the quantity one measures in an experiment is amplitude (for example, the amplitude of air pressure variations), and since power (what we have been loosely calling intensity) is proportional to the square of the amplitude, we have
of a bel, and is denoted dB. Thus, a difference of 5 bels is the same as a difference of 50 decibels. Oftentimes the quantity one measures in an experiment is amplitude (for example, the amplitude of air pressure variations), and since power (what we have been loosely calling intensity) is proportional to the square of the amplitude, we have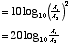
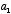 is the amplitude of one sound and
is the amplitude of one sound and 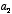 is the amplitude of the other.
is the amplitude of the other. 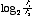 .
.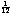 -octave, so the ratio between frequencies for each semitone is
-octave, so the ratio between frequencies for each semitone is 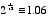 , or a 6% increase. Each time you raise a half-step, you multiply the frequency by about 1.06 to get the next note, and after you have done this 12 times you have multiplied by a factor of two. A full piano keyboard has 88 keys, and thus 7
, or a 6% increase. Each time you raise a half-step, you multiply the frequency by about 1.06 to get the next note, and after you have done this 12 times you have multiplied by a factor of two. A full piano keyboard has 88 keys, and thus 7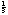 octaves, ranging from 27.5 Hz at the lowest A to 4186 Hz at the highest C.
octaves, ranging from 27.5 Hz at the lowest A to 4186 Hz at the highest C.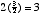 times the fundamental of C; thus, the second harmonic of G exactly aligns with the third harmonic of C. But this still doesn’t answer all of our questions. What if we were to just play two pure tones that don’t have any harmonics. We still get dissonance when they are next to each other in frequency. Why? The answer seems to be that it has something to do with critical bandwidth--i.e, the region over which frequencies significantly interact within a nerve fiber, which is about
times the fundamental of C; thus, the second harmonic of G exactly aligns with the third harmonic of C. But this still doesn’t answer all of our questions. What if we were to just play two pure tones that don’t have any harmonics. We still get dissonance when they are next to each other in frequency. Why? The answer seems to be that it has something to do with critical bandwidth--i.e, the region over which frequencies significantly interact within a nerve fiber, which is about 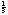 -octave. As shown in figure 4, the degree of perceived consonance between two tones depends on their relation to the critical bandwidth. If they are further apart than the critical bandwidth, then they are perceived to be consonant, but if within the critical bandwidth they are perceived dissonant. Of course as the two tones become even closer to one another they again become consonant. Thus, there seems to be a relation between dissonance and the bandwidth of frequency-tuned mechanisms in the cochlea and auditory nerve, but what interactions occur exactly that give rise to the percept of dissonance, and how this is processed and represented by the nervous system, is currently unknown.
-octave. As shown in figure 4, the degree of perceived consonance between two tones depends on their relation to the critical bandwidth. If they are further apart than the critical bandwidth, then they are perceived to be consonant, but if within the critical bandwidth they are perceived dissonant. Of course as the two tones become even closer to one another they again become consonant. Thus, there seems to be a relation between dissonance and the bandwidth of frequency-tuned mechanisms in the cochlea and auditory nerve, but what interactions occur exactly that give rise to the percept of dissonance, and how this is processed and represented by the nervous system, is currently unknown.