Degrees, radians, retinal size and sampling
Bruno A. Olshausen
Psych 129 - Sensory processes
When we open our eyes, an image of the world is projected onto the retinae. The intensity at each point in the image is converted to voltage by photoreceptors arrayed across each retina, and thus begins our perception of the world. In order to get a better understanding of this process, it is helpful to know how many photoreceptors or ganglion cells are sampling a given object or region in the image. This tells us the resolution at which an object is represented, which in turn limits how much of its structure can be perceived (analogous to having a high-resolution or low-resolution computer display). Here, we show how to compute the resolution at which an object is represented on the retina, and we discuss its implications for perception.
Degrees and radians
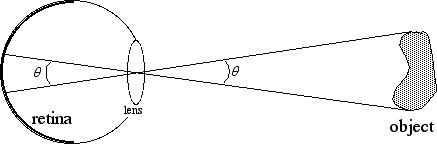
A convenient way to measure the distance between two points along the retina, or the distance between two points in visual space, is in terms of the angle between them. This angle is constructed by drawing a line from one point to the center of the lens/cornea, and then back to the other point, as shown in Figure 1.

Figure 1: Measuring distance along the retina or in visual space in terms of angle.
The reason this is a convenient measure of distance is because the size of an object on the retina and its size in the visual world are equivalent in terms of angle, so it saves us alot of conversion back and forth. If an object subtends 10 of visual space, it also subtends 10
of visual space, it also subtends 10 on the retina - simple as that.
on the retina - simple as that.
How do you compute the angle subtended by an object in the visual world? One way to do it exactly is with trigonometry, as shown in Figure 2. Take one-half the object size divided by the distance from the eye, and the inverse tangent of this ratio will give you half the angle. But there is a simpler, approximate way to do it using simple geometry - i.e., in terms of radians. Measuring an angle in radians basically tells you what fraction (or multiple) of the radius the object subtends in terms of arc length. Shown in Figure 3 is an arc length of one radian, equal to the length of the radius. If the object is small relative to the radius, then dividing its size by the radius will give an
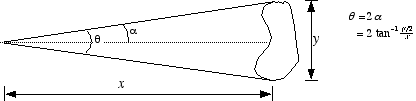
Figure 2: Trigonometric method for computing angle subtended by an object.
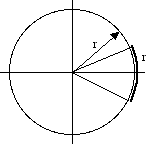
Figure 3: Geometric method for computing angle subtended by an object.
approximately correct angle in radians, even though the object doesn’t curve like the arc depicted in the figure. Thus, in terms of the notation in Figure 2 we have:
angle in radians 
 .
.
Once you have the angle in radians, you simply convert to degrees by multiplying by 180/ :
:
angle in degrees = angle in radians  deg/rad.
deg/rad.
To get a feel for the sizes of various object in degrees, the moon subtends about 0.5 degrees, your thumb subtends about two degrees (when held at arms length), and your average computer monitor subtends about 30 degrees (assuming you are viewing it from two feet away).
Once you have calculated the angle subtended by an object, now what do you do? Calculate resolution! But in order to do this, we need to know about the density of the retinal sampling lattice.
Sampling
There are two crucial stages of sampling that take place in the retina. One is via the photoreceptors (rods and cones) that initially transduce light into voltage and electrochemical signals. The other is via the retinal ganglion cells which sample the outputs of the photoreceptors (after being processed by the horizontal, bipolar, and amacrine cells). While the density of photoreceptors declines somewhat with eccentricity, the density of ganglion cells falls off even more sharply. There are about 130 million photoreceptors tiling the retina, and this information is summed into only one million ganglion cells. Thus, there is a net convergence or “fan-in” ratio of about 100:1. The signals conveyed by the one million ganglion cells are the sole statement that the cortex gets to “see” from the retinal image. Were they to be tiled evenly over the 2D image, they would provide an equivalent resolution of about 1000x1000 pixels for the entire visual field (which isn’t much!). Instead, they are arranged so as to obtain extremely high resolution in the fovea - sampling the photoreceptors in a one-to-one ratio - and then falling off with eccentricity, as depicted in Figure 4.
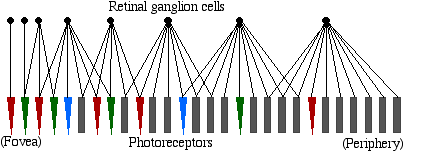
Figure 4: Retinal ganglion cell and photoreceptor sampling lattices, in one-dimension.
The exact manner in which resolution falls off is such that the spacing between retinal ganglion cells (along one dimension) increases linearly with eccentricity, as shown in Figure 5. This
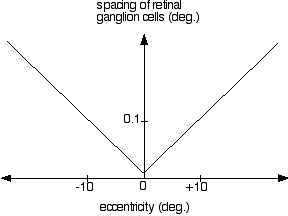
Figure 5: Ganglion cell spacing as a function of eccentricity.
relation can be described approximately with the function  , where
, where  is the spacing between adjacent retinal ganglion cells, in degrees, and E is eccentricity, also in degrees. (That this is so is really quite fascinating, from an engineering viewpoint, because it provides scale-invariance. As you look at the center of your hand, the number of ganglion cells falling on each of your finger tips will be about constant, independent of viewing distance. This feature conceivably makes it easier to recognize objects amidst variations in size on the retina.)
is the spacing between adjacent retinal ganglion cells, in degrees, and E is eccentricity, also in degrees. (That this is so is really quite fascinating, from an engineering viewpoint, because it provides scale-invariance. As you look at the center of your hand, the number of ganglion cells falling on each of your finger tips will be about constant, independent of viewing distance. This feature conceivably makes it easier to recognize objects amidst variations in size on the retina.)
Resolution and eccentricity
The number of samples subtending an object is what limits the resolution with which it is perceived. For example, when you look at your thumb just a few inches from your eye, many fine details such as the creases in the skin, hair, and structure of the fingernail can be perceived. Using the relations above, you should be able to deduce that there are about 50 ganglion cells sampling a 1 mm. region of your thumb (along one-dimension) when held 5 inches from your eye. That means each cone is subtending about 20 microns! So, any changes in reflectance occurring at that spatial scale or above can be perceived. If you move your thumb a bit away from the center of gaze, then it is now being sampled by fewer ganglion cells, each of which is summating over a several photoreceptors. Hence, the 20 microns details previously perceived at the center of gaze are being effectively neurally blurred and can not be perceived as a result. With each doubling in eccentricity, the number of samples subtending your thumb (along one-dimension) will be decreasing approximately by one-half. By the time you get to 10 degrees eccentricity, only 1/10 the number of ganglion cells will be subtending your thumb, so only details larger than 200 microns will be perceived.
In the 1970’s, Stuart Anstis measured the minimum size that characters need to be printed in order to be perceived, as a function of their eccentricity on the retina. Interestingly, he found that the minimum size scaled linearly with eccentricity, similar to Figure 5, but with a different slope. Roughly, the relation he found was  , where S denotes the minimum recognizable size of the character. Referring back to our equation for retinal ganglion cell spacing, this implies that a character needs to subtend a region of approximately 4x4 ganglion cells, independent of where it falls on the retina. (Even more interesting is the fact that George Sperling has independently shown that the efficiency of character recognition, in terms of spatial-frequency content, is maximum at just under 2 cycles/per object. According to the Nyquist sampling theorem then, about 4 samples across would be needed to carry this information. Thus, three independent measurements, together with computational theory, are totally consistent!) Whether this can be generalized to other more complicated shapes, such as faces, has yet to be tested rigorously however.
, where S denotes the minimum recognizable size of the character. Referring back to our equation for retinal ganglion cell spacing, this implies that a character needs to subtend a region of approximately 4x4 ganglion cells, independent of where it falls on the retina. (Even more interesting is the fact that George Sperling has independently shown that the efficiency of character recognition, in terms of spatial-frequency content, is maximum at just under 2 cycles/per object. According to the Nyquist sampling theorem then, about 4 samples across would be needed to carry this information. Thus, three independent measurements, together with computational theory, are totally consistent!) Whether this can be generalized to other more complicated shapes, such as faces, has yet to be tested rigorously however.