Psych 163
Fourier Analysis in Vision
The two-dimensional Fourier transform
- The Fourier transform may be extended to modalities other than time (e.g., space) and also to two-dimensions.
- The Fourier transform of an image,
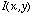 , is
, is
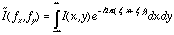
where 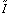 denotes the Fourier transform of I.
denotes the Fourier transform of I.
- Now the exponential function inside the integral corresponds to two-dimensional sine and cosine gratings at different spatial-frequencies and orientations, rather than simply one-dimensional waveforms at different frequencies.
- The spatial-frequency of a grating is given by the square-root of the sum of the squares of its horizontal and vertical components:
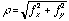
- The orientation of a grating is defined as the inverse tangent of the ratio of the vertical frequency component to the horizontal frequency component:
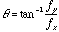
- Thus, each point in the 2D Fourier plane,
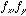 , corresponds to a grating of a different spatial-frequency,
, corresponds to a grating of a different spatial-frequency, 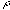 , and orientation,
, and orientation, 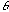 . Low-frequency gratings correspond to large-scale undulations in luminance across the image (e.g., a natural scene might be brighter in the upper half of the image and darker in the lower half of the image, which could be described with a low-frequency grating in the vertical direction:
. Low-frequency gratings correspond to large-scale undulations in luminance across the image (e.g., a natural scene might be brighter in the upper half of the image and darker in the lower half of the image, which could be described with a low-frequency grating in the vertical direction: 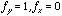 ). High-frequency gratings correspond to small-scale undulations in luminance (e.g., due to fine textures such as hair or grass).
). High-frequency gratings correspond to small-scale undulations in luminance (e.g., due to fine textures such as hair or grass).
Power spectrum of natural images
- First, beware that Fourier analysis is not as natural a thing to do for images as it is for sound. This is because sounds in the natural environment are often created by vibrating membranes, and so an analysis of the different frequency components of a sound is often useful in parsing the different components of an auditory scene. But, images are not typically created by oscillatory variations in luminance across space. So, why bother applying such a formalism to images in the first place? The answer is that Fourier analysis still gives us useful insights about the structure of images, as well as the operations performed by various information processing strategies on images.
- David Field (ca. 1987) measured the power spectrum of many natural images and observed that nearly all have the universal characteristic of exhibiting a
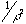 power spectrum (or
power spectrum (or 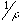 amplitude spectrum). This provides a useful, compact way of describing the autocorrelation function of natural images, since the power spectrum is just the 2D Fourier transform of the autocorrelation function. (The autocorrelation function just measures all of the pairwise correlations between pixel values in the image as a function of their spatial separation in the image:
amplitude spectrum). This provides a useful, compact way of describing the autocorrelation function of natural images, since the power spectrum is just the 2D Fourier transform of the autocorrelation function. (The autocorrelation function just measures all of the pairwise correlations between pixel values in the image as a function of their spatial separation in the image:
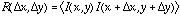 .
.
Without much trouble, you should be able to prove the following relation:
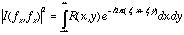 .)
.)
- The fact that this is so reflects the fact that natural images possess, to some extent, scale-invariant structure. This means that if you look at a natural scene with a camera with a variable zoom lens, there will be equal amounts of structure at all scales independent of the setting of the zoom. In Fourier terms, this implies that any spatial-frequency band with the same octave bandwidth (meaning the ratio of the highest to the lowest frequency of the band is constant) will have an equal amount of energy. That is,
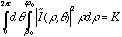
for any  . It is not difficult to prove that the only
. It is not difficult to prove that the only 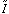 that satisfies this relation is one that falls as
that satisfies this relation is one that falls as 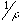 in frequency.
in frequency.
- As we shall see later in the course, it appears that the visual system knows about this aspect of natural images, and that evolution has designed early stages of the visual system so as to efficiently code images with
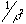 power spectrum.
power spectrum.
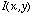 , is
, is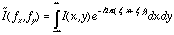
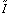 denotes the Fourier transform of I.
denotes the Fourier transform of I.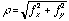
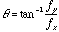
 , corresponds to a grating of a different spatial-frequency,
, corresponds to a grating of a different spatial-frequency, 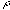 , and orientation,
, and orientation, 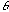 . Low-frequency gratings correspond to large-scale undulations in luminance across the image (e.g., a natural scene might be brighter in the upper half of the image and darker in the lower half of the image, which could be described with a low-frequency grating in the vertical direction:
. Low-frequency gratings correspond to large-scale undulations in luminance across the image (e.g., a natural scene might be brighter in the upper half of the image and darker in the lower half of the image, which could be described with a low-frequency grating in the vertical direction: 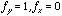 ). High-frequency gratings correspond to small-scale undulations in luminance (e.g., due to fine textures such as hair or grass).
). High-frequency gratings correspond to small-scale undulations in luminance (e.g., due to fine textures such as hair or grass).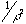 power spectrum (or
power spectrum (or 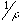 amplitude spectrum). This provides a useful, compact way of describing the autocorrelation function of natural images, since the power spectrum is just the 2D Fourier transform of the autocorrelation function. (The autocorrelation function just measures all of the pairwise correlations between pixel values in the image as a function of their spatial separation in the image:
amplitude spectrum). This provides a useful, compact way of describing the autocorrelation function of natural images, since the power spectrum is just the 2D Fourier transform of the autocorrelation function. (The autocorrelation function just measures all of the pairwise correlations between pixel values in the image as a function of their spatial separation in the image: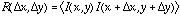 .
.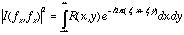 .)
.)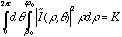
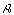 . It is not difficult to prove that the only
. It is not difficult to prove that the only 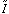 that satisfies this relation is one that falls as
that satisfies this relation is one that falls as 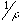 in frequency.
in frequency.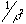 power spectrum.
power spectrum.