Psych 163
Linear receptive field models
Retina
- Since the physiological recordings of retinal ganglion cells by Hartline, Barlow, and Kuffler during the 1950’s, it has been well known that these neurons signal the spatial differences in light intensity falling upon the retina. This is accomplished by the so-called “center-surround” organization of the receptive field, in which its excitatory and inhibitory subfields are organized into circularly symmetric regions.
- The shapes of these receptive fields have been modeled by at least two different types of functions. One is the difference-of-Gaussians (DOG) function and the other is the Laplacian-of-Gaussian (LOG) function. The DOG model simply uses the difference of two 2D Gaussians to model the receptive field shape. The LOG model was proposed by Marr and Hildreth and uses the second spatial-derivative (hence the term Laplacian) of a Gaussian to model the receptive field shape. Both of these functions capture reasonably well the “Mexican hat” shape of retinal ganglion cell receptive fields.
- We can think of the receptive field shape of a retinal ganglion cell as the linear spatial weighting function of the cell. That is, we can model the retinal ganglion cell as a linear neuron, where the receptive field tells us what the weights are. Using the function
 to characterize the receptive field shape using either the DOG or LOG model, we compute the output of a model retinal ganglion cell as
to characterize the receptive field shape using either the DOG or LOG model, we compute the output of a model retinal ganglion cell as
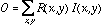 .
.
where  is the input image.
is the input image.
- For a whole array of retinal ganglion cells with identical receptive fields, we compute the output of each cell in the array as
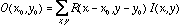
where  is the output of the retinal ganglion cell whose receptive field is centered at position
is the output of the retinal ganglion cell whose receptive field is centered at position  .
.
- Of course, the real situation in the retina is much more complicated, because the transformation from pixels to retinal ganglion cell outputs is mediated by many other neurons and complex synapses. But the above equations nevertheless provide a good first-order approximation of the function of these cells.
- There are two major varieties of center-surround receptive fields, on-center/off-surround and off-center/on-surround, depending on whether the central region is excitatory or inhibitory, respectively. It is widely thought that the reason for having these two different varieties is so that both positive and negative changes in intensity can be signaled with positive-only quantities (action potentials).
- The reason why the retina would compute such a function in the first place has been the subject of many different theories. One theory is that it provides a more efficient representation of the image because it eliminates redundancies due to the similarities of neighboring pixel values inherent in natural images. Another theory is that it signals the locations of edges, which is the first step in form or shape analysis.
Cortex
- Proceeding further up the visual pathway, one finds cells in the visual cortex (area V1) that are orientation-selective, meaning that they respond to spatial intensity changes only along a certain orientation. Such cells were named simple-cells and complex-cells by Hubel & Wiesel, who first described them in the early 1960’s (work for which they later won the Nobel prize). Here we focus on modeling the structure of simple-cells.
- Marcelja and Daugman (ca. 1980) have pointed out that the receptive fields of simple-cells are well-described with a Gabor function, which is simply a Gaussian modulated sinusoid. In one-dimension, this is expressed as

where  denotes the width of the Gaussian envelope,
denotes the width of the Gaussian envelope,  denotes the carrier frequency of the sinusoid, and
denotes the carrier frequency of the sinusoid, and  its phase. The larger we make
its phase. The larger we make for a fixed frequency
for a fixed frequency  , the more wobbles the function will have. In two-dimensions we have
, the more wobbles the function will have. In two-dimensions we have

where  and
and  , and
, and  is the orientation of the Gaussian envelope. Note that
is the orientation of the Gaussian envelope. Note that  is usually chosen to be the same as the orientation of the sinusoidal carrier,
is usually chosen to be the same as the orientation of the sinusoidal carrier,  .
.
- Thus, we could think of simple-cells in the visual cortex as representing the result of computing the inner-product between a Gabor function and the image at each position in the image, for each orientation (
 ) and spatial-frequencie (
) and spatial-frequencie ( ):
):
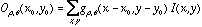
where  denotes a Gabor function of spatial-frequency
denotes a Gabor function of spatial-frequency  and orientation
and orientation  as defined above. Of course the neural images
as defined above. Of course the neural images  are all intertwined with each other over the cortex, preserving topography globally and grouping into orientation columns locally.
are all intertwined with each other over the cortex, preserving topography globally and grouping into orientation columns locally.
- The Gabor function is so-named because it was first discussed by Denis Gabor, a communication theorist, in the 1940’s (no relation to Zsa-Zsa). These filters are currently used in image processing, and form useful representations for compression as well as for image analysis and recognition.
 to characterize the receptive field shape using either the DOG or LOG model, we compute the output of a model retinal ganglion cell as
to characterize the receptive field shape using either the DOG or LOG model, we compute the output of a model retinal ganglion cell as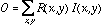 .
. is the input image.
is the input image. 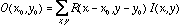
 is the output of the retinal ganglion cell whose receptive field is centered at position
is the output of the retinal ganglion cell whose receptive field is centered at position  .
. 
 denotes the width of the Gaussian envelope,
denotes the width of the Gaussian envelope,  denotes the carrier frequency of the sinusoid, and
denotes the carrier frequency of the sinusoid, and  its phase. The larger we make
its phase. The larger we make for a fixed frequency
for a fixed frequency  , the more wobbles the function will have. In two-dimensions we have
, the more wobbles the function will have. In two-dimensions we have
 and
and  , and
, and  is the orientation of the Gaussian envelope. Note that
is the orientation of the Gaussian envelope. Note that  is usually chosen to be the same as the orientation of the sinusoidal carrier,
is usually chosen to be the same as the orientation of the sinusoidal carrier,  .
. ) and spatial-frequencie (
) and spatial-frequencie ( ):
):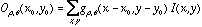
 denotes a Gabor function of spatial-frequency
denotes a Gabor function of spatial-frequency  and orientation
and orientation  as defined above. Of course the neural images
as defined above. Of course the neural images  are all intertwined with each other over the cortex, preserving topography globally and grouping into orientation columns locally.
are all intertwined with each other over the cortex, preserving topography globally and grouping into orientation columns locally.